Posted on | In

常用软件

  • 好压
  • QQ
  • 福昕阅读器
  • 有道词典
  • Office2016
  • visio

编译环境

  • Sublime
  • Atom
  • Visual Studio
  • Qt
  • Code::blocks

  • Eclipse

  • GIT

  • Hexo
  • G++

EDA工具

  • altium Designer
  • Multism
  • Vivado
  • ISE

  • quartus

  • Iar for ARM

  • KEIL C51 & ARM
  • CodeWarrior

Math

  • Matlab
  • Mathematic
  • Lingo

Posted on

TI公司现在主推四大系列DSP
1）C5000系列（定点、低功耗）：C54X，C54XX，C55X 相比其它系列的主
要特点是低功耗，所以最适合个人与便携式上网以及无线通信应用，如手
机、PDA、GPS等应用。处理速度在80MIPS–400MIPS之间。C54XX和C55XX
一般只具有McBSP同步串口、HPI并行接口、定时器、DMA等外设。
值得注意的是C55XX提供了EMIF外部存储器扩展接口，可以直接使用SDRAM，
而C54XX则不能直接使用。两个系列的数字IO都只有两条。
2）C2000系列（定点、控制器）：C20X，F20X，F24X，F24XX ，C28x该系列芯片具有大量外设资源，如：A/D、定时器、各种串口（同步和异步），
WATCHDOG、CAN总线/PWM发生器、数字IO脚等。是针对控制应用最佳化
的DSP，在TI所有的DSP中，只有C2000有FLASH，也只有该系列有异步
串口可以和PC的UART相连。
3）C6000系列：C62XX，C67XX，C64X 该系列以高性能著称，最适合宽带
网络和数字影像应用。32bit，其中：C62XX和C64X是定点系列，C67XX
是浮点系列。该系列提供EMIF扩展存储器接口。该系列只提供BGA封
装，只能制作多层PCB。且功耗较大。同为浮点系列的C3X中的VC33现在
虽非主流产品，但也仍在广泛使用，但其速度较低，最高在150MIPS。
4）OMAP系列：OMAP处理器集成ARM的命令及控制功能，另外还提供DSP
的低功耗实时信号处理能力，最适合移动上网设备和多媒体家电。

其他系列的DSP曾经有过风光，但现在都非TI主推产品了，除了C3X系列
外，其他基本处于淘汰阶段，如：
C3X的浮点系列：C30，C31，C32
C2X和C5X系列：C20，C25，C50
每个系列的DSP都有其主要应用领域.

Posted on | In

在分析连续周期信号和非周期信号时，将连续信号分别表示为虚指数$e^{jn\omega_0t}$和$e^{j\omega t}$,从而实现连续信号的Fourier变换和信号频域分析。类似的是，可以将离散序列表示为$e^{jm\Omega_0t}$和$e^{j\Omega t}$,从而引入离散周期序列的Foourier级数（DFS)和离散非周期序列的Fourier变换(DTFT)

1. 离散傅里级数(DFS)

周期为N的离散序列 $\tilde x[k]$可以由N项虚指数序列$ \{ e^{jm\Omega0k};m = 0,1,2,3,\cdots\}$的线性加权之和
$$ \tilde x[k] = \frac{1}{N}\sum_{m=0}^{N-1}\tilde X[m]e^{j\frac{2\pi}{N}mk} = \frac{1}{N} \sum_{m= < N >} W_N^{mk}$$

由虚指数序列的正交特性，可以得 到系数$\tilde X[m]$为
$$ \tilde X[m] = \sum_{k = 0}^{N-1}\tilde x[k]e^{-j\frac{2\pi}{N}mk}=\sum_{k = < N >}\tilde x[k]W_N^{-mk} $$

2.关于 DFS 的一些性质

基本和连续信号的一致

1. 线行特性，满足叠加定理

2. 位移特性

时域位移特性:$\tilde x[k+n] \stackrel{\text{DFS}}\to W_N^{-mn}\tilde 2X[m]$
频域位移特性：$ W_N^{ml}\tilde x[k] \stackrel{\text{DFS}}\to \tilde X[m+l] $

3. 对称特性

关于对称特性需要注意的是实周期序列$\tilde x[k]$的频谱$\tilde X[m]$的实部为m的偶函数，虚部为m的奇函数，也就是幅度谱m的偶函数，相位谱为m奇函数

4. 周期卷积特性

离散时间Fourier变换

周期序列通过离散Fourier级数实现信号从时域到频域的映射，而非周期序列正是通过离散时间Fourier变换实现信号从时域到频域的映射。

其正反变换公式为：
$$\begin{align} X(e^{j\Omega}) &= \sum_{k=-\infty}^{\infty}x[k]e^{-j\Omega k}\\
x[k] &=\frac{1}{2\pi} \int_{<2\pi>}X(e^{j\Omega})e^{j\Omega}d\Omega \end{align}$$

Posted on | In

江湖传言，STM32的硬件I2C一直有bug，最近面临做四旋翼的芯片选型问题,原文

下面的函数中有一个BUG, 也就是SR2不能用WHILE来轮询,而应直接读出.如下面代码段, 因此,在这里说的这是STM32的BUG其实是我的代码的错误:

1
2
3
I2C2->DR = inerAddress[1];
while( (I2C2->SR1&Q_I2C_SR1_BIT_BTF)==0 );
I2C2->SR2;   // 正解

一直都不相信STM32的I2C接口会存在问题，因为工作经验无数次告诉我，嵌入式系统设计中的99.999%的问题不会是由于MCU本身的设计问题所引起,绝大部分都是硬件工程师或软件工程师的某个设计缺陷所造成的. 这次的设计经历也不例外.

由于终于可以抽多点时间用于设计STM32的I2C的软件接口, 因此, 决定重构之前用于主从STM32通讯所用的I2C模块（基于I2C中断+状态机收发）。I2C的中断发送模块很快就重构完毕并且强化了错误处理和I2C总线hang的自恢复功能代码模块（I2C BUS Hang：也就是SDA 和SCL都被某Slave DEVICE拉低，大部分发生在主机接收从机传过来的数据包的最后一个字节的数据时，没有发送P（停止位）所造成的，这时Slave device （EEPROM）因为接收不到P，从而会DEAD LOOP地发送数据给主机，在主机方向看，I2C总线就相当于一直处于BUSY的状态，也就是网上问得最多的关于I2C的问题-I2C总线TMD的怎么会突然间死掉了、BUSY了、HANG的原因。）。

本以为I2C中断读模块也会很顺利地完成，但是却被卡住了一整天，只要加一个断点，在大部份代码处加无所谓，读FUN每次都正确执行，但只要全速运行，就只能运行一次，然后就过不去了，而且过不去的地方并不固定。由于DUBEG得有点集中不了精力，于是就做好问题的Brainstrom的笔记，放了下，晚上出差到深圳，到客户处做系统需求的讨论会，主要是上位机部分的。然后第二天晚上又赶回来，在车上的半梦半觉中让潜意思去思考。回到家后，选择在我的生物钟的最佳的时侯，晚上10点。开始重新在问题的Brainstorm处接着DUBGE。WORK PLAN如下：

  1. 把程序恢复到测试I2C写的测试用例状态，PASS。
  2. 一小段代码就DEBUG一次的步步为营方法，按之前的思路把代码加入到读的模块（忽略防守代码，只加入必需的功能代码）。都OK后，全速运行，XXX，又卡住了。细过了一片读模块。PASS。于是进入计划中的（3）
  3. 全速运行，然后在可能卡住的地方加上断点，而不是之前的先加断点，然后运行的方式（这种方式，已确认PASS）：
    加了几处后，发现程序是在下面代码处卡住的：


但是奇怪了，每次我只要在箭头指向的语句后加上断点，每次都能PASS。于是知道要到 I2C_CheckEvent 函数中就能找到问题的原因了，于是做下面的几步，目的是把包含I2C_CheckEvent Fun的链接库中的stm32f10x_i2c.o排除掉,而把stm32f10x_i2c.c加入到项目中,使得DEBUG时能进入到 I2C_CheckEvent Fun 中去.

于是全速运行，然后在 stm32f10x_i2c.c中加上断点，终于捕捉到问题点了，分析如下图所示：


1
2
3
4
5
6
7
8
9
10
#define vu32 volitile unsigned long long 
/* Read the I2Cx status register */
//  flag1 = I2Cx->SR1;             // 原代码
//  flag2 = I2Cx->SR2;            //原代码
//  flag2 = flag2 << 16;           //原代码

 /* Get the last event value from I2C status register */
  //lastevent = (flag1 | flag2) & FLAG_Mask; //原代码
 lastevent = (vu32)( (vu32)(I2Cx->SR1) | ((vu32)(I2Cx->SR2) << (vu32)16) ); //qzm为了确认而加入的，实际效果和用库的是一样的结果。
 lastevent &= (vu32)FLAG_Mask; //qzm为了确认而加入的，实际效果和用库的是一样的结果。

为了确认，我也把 Fun中的所有变量改为以v开头的，以确保不被编译器所优化掉，编译代码也不作任何的优化。但是全速时I2C获得的事件会多出个BTF位，而在一开始时如果先进入DEBUG，加上断点，然后运行，lastevent == 0x30001(之也说明了库代码是不存在BUG的）,如下图所示:

这应该是STM32 I2C硬件接口的BUG，解决方法如下：

把库中的I2C中断事件判定结合SR1和SR2的思路相反,我把读SR1和SR2明确地分了出现,并进行确认, PASS, 给模块加上防守代码,做好文档, 至此,模块的生命周期进入到白盒测试和黑盒测试阶段.

Posted on

hexo-math

A hexo plugin that uses MathJax to render math equations. Features:

  • Automatcially deploy and add reference to MathJax
  • Provide support to both MathJax’s inline math syntax and math tags

(See a Chinese version of this document here) Information in that post is out-dated

Install

npm install hexo-math –save

See Migration Note if you are upgrading from an older version.

Usage

You can use MathJax’s inline math syntax directly. But always remember to escape any special characters by adding a

before it.
1
2
3
4
5
6
LaTex equations usually contains tones of special characters like ```\```, which makes it painful to escape them one by one. In such cases, you can use hexo-math's tags to make your life easier.

**MathJax Inline:**

```markdown
Simple inline $a = b + c$.

MathJax Block:

1
2
3
4
$$\frac{\partial u}{\partial t}
= h^2 \left( \frac{\partial^2 u}{\partial x^2} +
\frac{\partial^2 u}{\partial y^2} +
\frac{\partial^2 u}{\partial z^2}\right)$$

Tag:

Single line content will be parsed as inline math (same as $...$):

1
This equation {% math %}\cos 2\theta = \cos^2 \theta - \sin^2 \theta =  2 \cos^2 \theta - 1 {% endmath %} is inline.

Multiple line content will be parsed as block math (same as $$...$$)

1
2
3
4
5
6
7
{% math %}
\begin{aligned}
\dot{x} & = \sigma(y-x) \\
\dot{y} & = \rho x - y - xz \\
\dot{z} & = -\beta z + xy
\end{aligned}
{% endmath %}

Deprecated since 2.0.0

Tag Block:

1
2
3
4
5
6
7
{% math_block %}
\begin{aligned}
\dot{x} & = \sigma(y-x) \\
\dot{y} & = \rho x - y - xz \\
\dot{z} & = -\beta z + xy
\end{aligned}
{% endmath_block %}

Migration Note

Migrating to 2.0.0

  • math_block is deprecated (but still usable. This won’t break your site)
  • math block is used to handle both inline and block math due to breaking changes made since Hexo 3.x. (This will break your site if you’re using math block)

Since Hexo 3.x, nunjucks is used as tag engine instead of swig. Syntax like this won’t work any more:

1
{% math \frac{|ax + by + c|}{\sqrt{a^{2}+b^{2}}} %}

Instead, you should use open and close tag since this version:

1
{% math %}\frac{|ax + by + c|}{\sqrt{a^{2}+b^{2}}} {% endmath %}

Change all your math tags accordingly.

Migrating to 1.0.6

!!!IMPORTANT!!!

Since 1.0.6, hexo-math uses a diffrent approach to inject MathJax into your site. MathJax will be injected on-the-fly and on-demand. This means:

  • You are no longer required to run hexo math install
  • MathJax will not be loaded on pages without math tags allowing faster loading speed.

If you have run hexo math install before, please do run:

1
$ hexo math

This will clean up previous installation. Or you can re-install your theme if for some reason this does not work.

From 1.0.4 to 1.0.5 (Support Hexo 3.0)

Hexo 3.0 introduces multiple breaking changes. Versions before 1.0.5 won’t work with it.
The following changes are made since 1.0.5 to adapt the new 3.0 API:

  • Block math tag renamed from math-block to math_block

From 1.0.3 and before

Since 1.0.4, MathJax scripts will be injected in <body> section instead of <head> section.
Before you update hexo-math to newer version, you should run:

$ hexo math uninstall

After hexo-math is updated, run install again:

$ hexo math install

Development

Test

To run the test suit, first you should install dependencies for the test site:

1
2
> $ cd .test-site
> $ npm install

Then run npm test from hexo-math‘s root dir.

Add post specs

In .test-site/source/_post folder, add a pair of file for each test cases:

  • [test-case-name].md
  • [test-case-name].md.expected

The .md file contains the Markdown source of a post and the .expected file contains expected HTML rendered from the source.

If a test case is added to address certian issues, the issue id should be added to the .md‘s front matter section:

1
2
3
4
5
6
7
title: "Tag Escpae"
date: 2015-04-21 02:47:19
tags:
issues:
- 10
---
{% math %} |a|<1 {% endmath %}

Posted on | In

What’s 离散时间信号

信号可以表示为一个或多个自变量的函数，在信号的分类中，自变量连续的称为连续时间信号，自变量离散变化的信号称为离散时间信号。离散时间信号通常也被称为（离散）序列。另外，在通用计算机中，信号的幅度值只能去有限个离散值。这样的离散时间信号又称为数字信号

离散序列的$x[k]$可以用图形表示，如下图所示，其中横轴表示整数$k$，纵向线段的长短表示信号幅度的大小。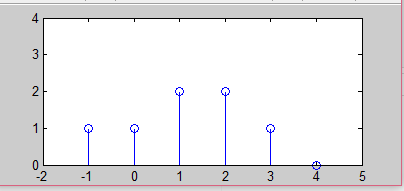
离散序列的图形表示
离散序列$x[k]$ 也可以由矩阵形式表示。上图表示的离散序列可以表示为矩阵形式：
$$ \begin{align}
&{x}[k]=\{1,1,2,2,1,0;k = -1,0,1,2,3,4\} \\
&x[k]=\{1,\hat1,2,2,1,1\}
\end{align}$$
上式中的箭头$\downarrow$ 表示的是$k=0$所在的位置。如果没有特殊说明，约定$k = 0$作为起点
离散序列$x[k]$也可以由解析表达式表示，如指数序列
$$x[k] = 3(2)^k,k\in Z $$

常用序列

1.单位脉冲序列（unit impulse sequence）

单位脉冲序列的定义是:
$$\delta[k] =
\begin{cases}
1,&k=0\\
0,&k \neq 0\\
\end{cases}$$
位移_n_个样本之后的单位脉冲序列定义为
$$\delta[k] =
\begin{cases}
1,&k=n\\
0,&k \neq n\\
\end{cases}$$

显然任何离散序列$x[k]$都可以利用单位脉冲序列来表示，即:
$$x[k]=\sum_n{x[k]\delta [k-n]}$$
例如${x}[k]=\{1,1,2,2,1,0;k = -1,0,1,2,3,4\}$可以表示为$x[k]=\delta[k+1]+\delta[k]+2\delta[k-1]+2\delta[k-2]+\delta[k-3]$

2.单位阶跃序列(unit step sequence)

单位阶跃序列的定义为:
$$\delta[k] =
\begin{cases}
1,&k\geqslant 0\\
0,&k<0\\
\end{cases}$$
单位阶跃信号和单位脉冲信号$\delta[k]$之间的关系是
$$u[k] = \sum_{n=-\infty}^{k}\delta{n}\\
\delta[k] = \nabla u[k] = u[k] - u[k-1]$$
由此得出：

  • 单位节约序列$u[k]$是单位脉冲序列$\delta[k]$的累加
  • 单位脉冲序列$\delta[k]$是单位阶跃序列$u[k]$的后向差分

3.矩阵序列（rectangle sequence）

长度为N的矩形序列（rectangle sequence）定义为：
$$ R_N[k]=\begin{cases}1,&{0\leqslant{k}\geqslant{N-1}}\\
0,&\text{其他}\end{cases}$$
矩形序列$R_N[k]$可用单位脉冲序列$\delta[k]$或单位阶跃序列$u[k]$表示为
$$ R_{N}[k]=u[k]-u[k-N]=\sum_{n=0}^{N-1}\delta[k-n]$$

4.指数序列

5.正弦型序列

6.虚指数序列

序列的卷积与相关运算

1.序列的卷积

序列的卷积(convolution)定义为
$$y[k] = x_1[k] * x_2[k] = \sum_{n=-\infty}^{\infty}x_1[n]x_2[k]$$
对于序列的卷积运算的物理意义有一遍比较好的解释卷积

从另一种意义上讲，线性卷积y[k]是h[k]去加权x各个时延版本在求和
或者，各个时刻的激励x在k时刻的冲激响应的叠加，即激励信号对系统H的零状态响应

序列的卷积运算满足：

  • 交换率
  • 结合律
  • 分配率
  • 位移特性

2.序列相关运算

离散时间系统

离散时间系统可对一个已知的输入序列进行处理，从而产生一个满足特定需求的输出序列
系统建立了输入和输出之间的关系，即，$y[k]=T\{x[k]\}$

系统分类

  • 线性系统 输入于输出均满足均匀性和叠加性
  • 非时变系统
  • 因果系统
  • 稳定系统

如果一个系统满足线性和非时变特性，即称为LTI(Linear Time-Invariant)

离散LTI系统的响应及其特性

1. 系统的单位脉冲响应

离散LTI系统的单位脉冲响应定义为系统在零状态条件下，由单位脉冲响应$ \delta[k]$激励系统而产生的响应$h[k]$
$$ h[k] = T\{\delta[k]\}$$

单位脉冲信号$\delta[k]$ 作为输入信号仅在零时刻存在信号输入，所以单位脉冲响应$h[k]$显然和系统的输入和输出无关，只取决于系统本身的结构和参数，所以用来反映离散LTI系统的时域特性

2. 离散LTI系统的零状态响应

由于x[k]很容易表达为多个单位脉冲信号$\delta[k]$的叠加，所以离散LTI系统的零状态响应可用单位脉冲响应来表示
显然：
$$ x[k] = \sum_n x[ n ]\delta[k-n] $$
根据LTI系统的线性特性可以得到：
$$ y[k] = T\{x[k]\} = T\{\sum_n x[ n ]\delta[k-n]\} = \sum_n x[k].T\{\delta[k-n]\} $$
由于是时不变系统，上式也就变为
$$ y[k] = x[k] * \delta[k] $$

3. 离散LTI系统稳定的充要条件

$$ \sum_{k=-\infty}^{\infty}|h[k]| = S < \infty $$

也就是说任何信号的零状态响应都可以表示为该信号和该离散LTI系统单位脉冲响应的卷积

Posted on | In

mark一下马克飞翔的示例……

欢迎使用马克飞象

@(示例笔记本)[马克飞象|帮助|Markdown]

马克飞象是一款专为印象笔记（Evernote）打造的Markdown编辑器，通过精心的设计与技术实现，配合印象笔记强大的存储和同步功能，带来前所未有的书写体验。特点概述：

  • 功能丰富 ：支持高亮代码块、LaTeX 公式、流程图，本地图片以及附件上传，甚至截图粘贴，工作学习好帮手；
  • 得心应手 ：简洁高效的编辑器，提供桌面客户端以及离线Chrome App，支持移动端 Web；
  • 深度整合 ：支持选择笔记本和添加标签，支持从印象笔记跳转编辑，轻松管理。

[TOC]

Markdown简介

Markdown 是一种轻量级标记语言，它允许人们使用易读易写的纯文本格式编写文档，然后转换成格式丰富的HTML页面。 —— 维基百科

正如您在阅读的这份文档，它使用简单的符号标识不同的标题，将某些文字标记为粗体或者斜体，创建一个链接或一个脚注[^demo]。下面列举了几个高级功能，更多语法请按Ctrl + /查看帮助。

代码块

1
2
3
4
5
6
7
8
9
10
@requires_authorization
def somefunc(param1='', param2=0):
    '''A docstring'''
    if param1 > param2: # interesting
        print 'Greater'
    return (param2 - param1 + 1) or None
class SomeClass:
    pass
>>> message = '''interpreter
... prompt'''

LaTeX 公式

可以创建行内公式，例如 $\Gamma(n) = (n-1)!\quad\forall n\in\mathbb N$。或者块级公式：

$$ x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

1
2
$\Gamma(n) = (n-1)!\quad\forall n\in\mathbb N$
$$	x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

表格

Item Value Qty
Computer 1600 USD 5
Phone 12 USD 12
Pipe 1 USD 234

流程图

1
2
3
4
5
6
7
8
st=>start: Start
e=>end
op=>operation: My Operation
cond=>condition: Yes or No?

st->op->cond
cond(yes)->e
cond(no)->op

以及时序图:

1
2
3
Alice->Bob: Hello Bob, how are you?
Note right of Bob: Bob thinks
Bob-->Alice: I am good thanks!

提示：想了解更多，请查看流程图语法以及时序图语法。

复选框

使用 - [ ] 和 - [x] 语法可以创建复选框，实现 todo-list 等功能。例如：

☑- [x] 已完成事项
☐- [ ] 待办事项1
☐- [ ] 待办事项2

注意：目前支持尚不完全，在印象笔记中勾选复选框是无效、不能同步的，所以必须在马克飞象中修改 Markdown 原文才可生效。下个版本将会全面支持。

印象笔记相关

笔记本和标签

马克飞象增加了@(笔记本)[标签A|标签B]语法, 以选择笔记本和添加标签。 绑定账号后， 输入(自动会出现笔记本列表，请从中选择。

笔记标题

马克飞象会自动使用文档内出现的第一个标题作为笔记标题。例如本文，就是第一行的 欢迎使用马克飞象。

快捷编辑

保存在印象笔记中的笔记，右上角会有一个红色的编辑按钮，点击后会回到马克飞象中打开并编辑该笔记。

注意：目前用户在印象笔记中单方面做的任何修改，马克飞象是无法自动感知和更新的。所以请务必回到马克飞象编辑。

数据同步

马克飞象通过将Markdown原文以隐藏内容保存在笔记中的精妙设计，实现了对Markdown的存储和再次编辑。既解决了其他产品只是单向导出HTML的单薄，又规避了服务端存储Markdown带来的隐私安全问题。这样，服务端仅作为对印象笔记 API调用和数据转换之用。

隐私声明：用户所有的笔记数据，均保存在印象笔记中。马克飞象不存储用户的任何笔记数据。

离线存储

马克飞象使用浏览器离线存储将内容实时保存在本地，不必担心网络断掉或浏览器崩溃。为了节省空间和避免冲突，已同步至印象笔记并且不再修改的笔记将删除部分本地缓存，不过依然可以随时通过文档管理打开。

注意：虽然浏览器存储大部分时候都比较可靠，但印象笔记作为专业云存储，更值得信赖。以防万一，请务必经常及时同步到印象笔记。

编辑器相关

设置

右侧系统菜单（快捷键Ctrl + M）的设置中，提供了界面字体、字号、自定义CSS、vim/emacs 键盘模式等高级选项。

快捷键

帮助 Ctrl + /
同步文档 Ctrl + S
创建文档 Ctrl + Alt + N
最大化编辑器 Ctrl + Enter
预览文档 Ctrl + Alt + Enter
文档管理 Ctrl + O
系统菜单 Ctrl + M

加粗 Ctrl + B
插入图片 Ctrl + G
插入链接 Ctrl + L
提升标题 Ctrl + H

关于试用

马克飞象为新用户提供 10 天的试用期，试用期过后将不能同步新的笔记。之前保存过的笔记依然可以编辑。

反馈与建议

感谢阅读这份帮助文档。请点击右上角，绑定印象笔记账号，开启全新的记录与分享体验吧。

[^demo]: 这是一个示例脚注。请查阅 MultiMarkdown 文档 关于脚注的说明。 限制： 印象笔记的笔记内容使用 ENML 格式，基于 HTML，但是不支持某些标签和属性，例如id，这就导致脚注和TOC无法正常点击。

Posted on

创建矩阵的基本方法

直接输入法

注意：

  • 矩阵元素必须用[ ] 括住
  • 矩阵元素必须用逗号 或者空格分隔
  • 在 [ ]内矩阵的行和行之间必须用分号分隔

    矩阵元素：

  • 矩阵元素可以是matlab表达式，可以是实数，也可以是复数

    逗号和分号的作用：

  • 如同C语言一样可以作为指令间的分隔符。
  • 区别在于逗号结尾的语句在运行结束时立即显示语句的运行结果，而分号结尾的语句在运行结束之后不显示结果
    冒号的作用：
0%