What’s 离散时间信号
信号可以表示为一个或多个自变量的函数,在信号的分类中,自变量连续的称为连续时间信号,自变量离散变化的信号称为离散时间信号。离散时间信号通常也被称为(离散)序列。另外,在通用计算机中,信号的幅度值只能去有限个离散值。这样的离散时间信号又称为数字信号
离散序列的$x[k]$可以用图形表示,如下图所示,其中横轴表示整数$k$,纵向线段的长短表示信号幅度的大小。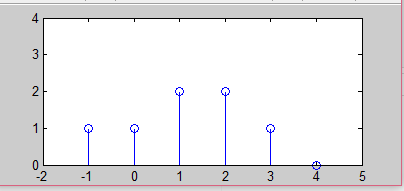
离散序列$x[k]$ 也可以由矩阵形式表示。上图表示的离散序列可以表示为矩阵形式:
$$ \begin{align}
&{x}[k]=\{1,1,2,2,1,0;k = -1,0,1,2,3,4\} \\
&x[k]=\{1,\hat1,2,2,1,1\}
\end{align}$$
上式中的箭头$\downarrow$ 表示的是$k=0$所在的位置。如果没有特殊说明,约定$k = 0$作为起点
离散序列$x[k]$也可以由解析表达式表示,如指数序列
$$x[k] = 3(2)^k,k\in Z $$
常用序列
1.单位脉冲序列(unit impulse sequence)
单位脉冲序列的定义是:
$$\delta[k] =
\begin{cases}
1,&k=0\\
0,&k \neq 0\\
\end{cases}$$
位移_n_个样本之后的单位脉冲序列定义为
$$\delta[k] =
\begin{cases}
1,&k=n\\
0,&k \neq n\\
\end{cases}$$
显然任何离散序列$x[k]$都可以利用单位脉冲序列来表示,即:
$$x[k]=\sum_n{x[k]\delta [k-n]}$$
例如${x}[k]=\{1,1,2,2,1,0;k = -1,0,1,2,3,4\}$可以表示为$x[k]=\delta[k+1]+\delta[k]+2\delta[k-1]+2\delta[k-2]+\delta[k-3]$
2.单位阶跃序列(unit step sequence)
单位阶跃序列的定义为:
$$\delta[k] =
\begin{cases}
1,&k\geqslant 0\\
0,&k<0\\
\end{cases}$$
单位阶跃信号和单位脉冲信号$\delta[k]$之间的关系是
$$u[k] = \sum_{n=-\infty}^{k}\delta{n}\\
\delta[k] = \nabla u[k] = u[k] - u[k-1]$$
由此得出:
- 单位节约序列$u[k]$是单位脉冲序列$\delta[k]$的累加
- 单位脉冲序列$\delta[k]$是单位阶跃序列$u[k]$的后向差分
3.矩阵序列(rectangle sequence)
长度为N的矩形序列(rectangle sequence)定义为:
$$ R_N[k]=\begin{cases}1,&{0\leqslant{k}\geqslant{N-1}}\\
0,&\text{其他}\end{cases}$$
矩形序列$R_N[k]$可用单位脉冲序列$\delta[k]$或单位阶跃序列$u[k]$表示为
$$ R_{N}[k]=u[k]-u[k-N]=\sum_{n=0}^{N-1}\delta[k-n]$$
4.指数序列
5.正弦型序列
6.虚指数序列
序列的卷积与相关运算
1.序列的卷积
序列的卷积(convolution)定义为
$$y[k] = x_1[k] * x_2[k] = \sum_{n=-\infty}^{\infty}x_1[n]x_2[k]$$
对于序列的卷积运算的物理意义有一遍比较好的解释卷积
从另一种意义上讲,线性卷积y[k]是h[k]去加权x各个时延版本在求和
或者,各个时刻的激励x在k时刻的冲激响应的叠加,即激励信号对系统H的零状态响应
序列的卷积运算满足:
- 交换率
- 结合律
- 分配率
- 位移特性
2.序列相关运算
离散时间系统
离散时间系统可对一个已知的输入序列进行处理,从而产生一个满足特定需求的输出序列
系统建立了输入和输出之间的关系,即,$y[k]=T\{x[k]\}$
系统分类
- 线性系统 输入于输出均满足均匀性和叠加性
- 非时变系统
- 因果系统
- 稳定系统
如果一个系统满足线性和非时变特性,即称为LTI(Linear Time-Invariant)
离散LTI系统的响应及其特性
1. 系统的单位脉冲响应
离散LTI系统的单位脉冲响应定义为系统在零状态条件下,由单位脉冲响应$ \delta[k]$激励系统而产生的响应$h[k]$
$$ h[k] = T\{\delta[k]\}$$
单位脉冲信号$\delta[k]$ 作为输入信号仅在零时刻存在信号输入,所以单位脉冲响应$h[k]$显然和系统的输入和输出无关,只取决于系统本身的结构和参数,所以用来反映离散LTI系统的时域特性
2. 离散LTI系统的零状态响应
由于x[k]很容易表达为多个单位脉冲信号$\delta[k]$的叠加,所以离散LTI系统的零状态响应可用单位脉冲响应来表示
显然:
$$ x[k] = \sum_n x[ n ]\delta[k-n] $$
根据LTI系统的线性特性可以得到:
$$ y[k] = T\{x[k]\} = T\{\sum_n x[ n ]\delta[k-n]\} = \sum_n x[k].T\{\delta[k-n]\} $$
由于是时不变系统,上式也就变为
$$ y[k] = x[k] * \delta[k] $$
3. 离散LTI系统稳定的充要条件
$$ \sum_{k=-\infty}^{\infty}|h[k]| = S < \infty $$
也就是说任何信号的零状态响应都可以表示为该信号和该离散LTI系统单位脉冲响应的卷积